WEEKLY CHALLENGES
Défi de la semaine | Indicación semanal
The two videos below show how scale can be used outside math class.
In the OK GO video, the music was slowed down 50% to record the complex movements
at half the speed. The song and moving images were sped up for the final video [source].
In the Star Size Comparison video, a dynamic scale comparison of objects in our solar system
(and beyond) helps us understand magnitude well beyond our experience as human-sized creatures.
In the OK GO video, the music was slowed down 50% to record the complex movements
at half the speed. The song and moving images were sped up for the final video [source].
In the Star Size Comparison video, a dynamic scale comparison of objects in our solar system
(and beyond) helps us understand magnitude well beyond our experience as human-sized creatures.
|
|
|
|
Week 12
Scale #scale #mathphoto15 Scale is a ratio that compares the size of one thing to another. It is what we are thinking about when we ask “how much bigger/smaller, taller/shorter, faster/slower.”
What are we looking for? The pictures included in this challenge will give you a good idea of the variety of ways we can encounter scale in our daily lives. How to Play: Take a photo. Post to Twitter or Instagram; adding a caption is highly encouraged. Use both hashtags: #mathphoto15 and #scale. Re-tweet and share others’ photos if you like. Encourage your friends to play!
How to View: Visit the #mathphoto15 Twitter stream any time. You can also view the stream on Flickr. At the end of each weekly challenge, images will be curated to a Storify and the link will be archived on the Summer Math Photo Challenge website. |
Semaine 12
Échelle #échelle #mathphoto15 L’échelle est une indication du rapport entre la grandeur de deux éléments. On y pense quand on se demande “Combien plus grand? plus petit? plus court? plus rapide? plus lent?”
Que cherchons nous? Les images qui accompagnent ce défi vous donnent de bonnes idées de situations où l’on pense “à l’échelle” dans notre vie de tous les jours. Comment jouer : Prendre une photo. Afficher la photo sur Twitter ou Instagram avec une légende. Utiliser les deux mots-clic : #mathphoto15 et #échelle. Décrire ce que l’on peut voir dans votre photo. Re-tweeter et partager les photos d’autres internautes si vous le voulez. Encourager vos amis à jouer avec vous! Comment apprécier : Visiter le fil Twitter #mathphoto15 en tout temps. Explorer aussi ce fil sur Flickr. À la fin de chaque défi de la semaine, les images seront organisées dans un Storify et le lien sera affiché sur le site DÉFI MATH PHOTO ÉTÉ 2015.
|
Semana 11
Escala #escala #mathphoto15 La escala es el la razón -el número- que proporciona la comparación de una cosa con otra. Es en lo que estamos pensando al preguntar "¿cuánto mayor/menor? (o más largo/corto, más rápido/lento...)"
¿Qué estamos buscando? Las imágenes que incluimos esta semana te darán buena idea de la variedad de maneras en las que podemos encontrar escala en nuestra vida diaria. ¿Cómo participar? Haz una foto. Súbela a Twitter o Instagram. Di dónde la tomaste, eso ayuda. Usa los dos hashtags #mathphoto15 y #escala. Retuitea las fotos de los otros y anima a tus amigos a participar. Como ver las fotos: Busca el hilo #mathphoto15 en cualquier momento. También puedes ver las fotos que se van subiendo a Flickr. Al final de la semana las mejores imágenes se seleccionarán en un Storify y se archivarán en la web del Desafío Foto-matemático del verano 2015. |
|
Week 11
Multiples & Groups #groups #mathphoto15 |
Semaine 11
Multiples/Groupes #groupes #mathphoto15 |
Semana 11
Múltiples/Grupos #grupos #mathphoto15 |
|
We utilize the ideas of multiples and groups when we are...
What are we looking for? This week we’re looking for things in our everyday lives that come in (or are purposefully organized into) groups. Shoes and glasses come in pairs. Dogs and cats have four legs. With open eyes and an inquisitive spirit you may be delighted by what you find! How to Play: Take a photo. Post to Twitter or Instagram; adding a caption is highly encouraged. Use both hashtags: #mathphoto15 and #groups and state what kind of unit you’re seeing, composed or partitioned. Re-tweet and share others’ photos if you like. Encourage your friends to play! How to View: Visit the #mathphoto15 Twitter stream any time. You can also view the stream on Flickr. At the end of each weekly challenge, images will be curated to a Storify and the link will be archived on the Summer Math Photo Challenge website. |
Nous exploitons l’idée des groupes et des multiples pour:
Que cherchons nous? Nous chercons des objets de notre environnement qui sont organisés (intentionnellement ou naturellement) en groupes. Des souliers et des lunettes viennent en paires. Les chats et les chiens ont 4 pattes. Cette semaine, gardez l’oeil ouvert et vous pourriez être étonnés par vos découvertes! Comment jouer: Prendre une photo. Afficher la photo sur Twitter ou Instagram avec une légende. Utiliser les deux mots-clic : #mathphoto15 et #groupes. Décrire ce que l’on peut voir dans votre photo. Re-tweeter et partager les photos d’autres internautes si vous le voulez. Encourager vos amis à jouer avec vous! Comment apprécier: Visiter le fil Twitter #mathphoto15 en tout temps. Explorer aussi ce fil sur Flickr. À la fin de chaque défi de la semaine, les images seront organisées dans un Storify et le lien sera affiché sur le site DÉFI MATH PHOTO ÉTÉ 2015. |
Utilizamos los conceptos de múltiplo y los agrupamientos cuando:
¿Qué estamos buscando? Esta semana buscamos a nuestro alrededor objetos que están organizados -a propósito o no- en grupos. Zapatos y gafas vienen en “pares”. Los perros y los gatos vienen con 4 patas. Abre bien los ojos, vas a alucinar con las cosas que encuentras. ¿Cómo participar?: Haz una foto. Súbela a Twitter o Instagram. Di dónde la tomaste, eso ayuda. Usa los dos hashtags #mathphoto15 y #grupos y explica qué es lo que ves, si está compuesto o repartido. Retuitea las fotos de los otros y anima a tus amigos a participar. Como ver las fotos: Busca el hilo #mathphoto15 en cualquier momento. También puedes ver las fotos que se van subiendo a Flickr. Al final de la semana las mejores imágenes se seleccionarán en un Storify y se archivarán en la web del Desafío Foto-matemático del verano 2015. |
|
Week 10
Geometric Solids #solids #mathphoto15 This week we’re looking for... examples of geometric solids, both polyhedra (objects with flat faces like cubes, prisms and pyramids) and non-polyhedra (objects where all or part of the surface is not flat, like cones, spheres, cylinders, etc) in the real, everyday world around us. We’re also looking for non-convex solids and real-world approximations -- things that do not have precise geometric names but hold volume and have surface area -- like a pot or a cup. Bonus points for cross sections and non examples!
How to Play: Take a photo. Post to Twitter or Instagram; adding a caption is highly encouraged. Use both hashtags: #mathphoto15 and #solids and describe what you’re seeing. Re-tweet and share others’ photos if you like. Encourage your friends to play! How to View: Visit the #mathphoto15 Twitter stream any time. You can also view the stream on Flickr. At the end of each weekly challenge, images will be curated to a Storify and the link will be archived on the Summer Math Photo Challenge website. |
Semaine 10
Solides géométriques #solides #mathphoto15 Cette semaine, nous sommes à la recherche...d’objets qui peuvent être décrits comme ayant une longueur, une profondeur et une largeur. Nous cherchons des exemples de solides géométriques, des polyèdres et des non-polyèdres dans notre environnement. Nous cherchons aussi des solides non convexes et des approximations, soit des objets qui n’ont pas de noms précis (cônes, sphères, cubes, prismes, cylindres...) mais qui ont un volume et une surface, tels une tasse ou un pot. Points bonis pour des sections de solides et des contre-exemples!
Comment jouer : Prendre une photo. Afficher la photo sur Twitter ou Instagram avec une légende. Utiliser les deux mots-clic : #mathphoto15 et #solides. Décrire ce que l’on peut voir dans votre photo. Re-tweeter et partager les photos d’autres internautes si vous le voulez. Encourager vos amis à jouer avec vous! Comment apprécier : Visiter le fil Twitter #mathphoto15 en tout temps. Explorer aussi ce fil sur Flickr. À la fin de chaque défi de la semaine, les images seront organisées dans un Storify et le lien sera affiché sur le site DÉFI MATH PHOTO ÉTÉ 2015. |
Semana 10
Sólidos geométricos #solids #mathphoto15 Esta semana buscamos... ejemplos de sólidos geométricos, sean poliedros (objetos con todas sus caras planas como cubos, prismas y pirámides) o no poliedros (alguna -o todas- sus caras es curva como conos, esferas, cilindros...) en el mundo cotidiano. También buscamos sólidos no convexos () y otras aproximaciones del mundo real -cosas que no tienen precisamente nombres geométricos pero que tienen volumen y superficie lateral- como una taza o una patata. Puntos extra para los que mezclen con temas de otras semanas y para los contraejemplos.
Cómo participar: Haz una foto. Publícala en Twitter o Instagram. Explíca qué ves o dónde la has hecho. Usa los hastags: #mathphoto15 and #solidos. Retuitea las fotos que te gusten y anima a tus amigos a participar. Como ver las fotos: Busca el hilo #mathphoto15 en cualquier momento. También puedes ver las fotos que se van subiendo a Flickr. Al final de la semana las mejores imágenes se seleccionarán en un Storify y se archivarán en la web del Desafío Foto-matemático del verano 2015. |
|
Week 9
Part/Whole Relationships #partwhole #mathphoto15 Last week we looked for and found units. A dozen eggs is a composed unit and so is a wall made out of bricks. We also found partitioned units like a loaf of bread, or a slab of bacon. This week we are looking at the related idea of part/whole relationships. Deborah Ball defines this kind of relationship (as it relates specifically to fractions) as “dividing a given unit (quantity) into some number of parts which includes:
How to Play: Take a photo. Post to Twitter or Instagram; adding a caption is highly encouraged. Use both hashtags: #mathphoto15 and #partwhole and describe what you’re seeing. Re-tweet and share others’ photos if you like. Encourage your friends to play! How to View: Visit the #mathphoto15 Twitter stream any time. You can also view the stream on Flickr. At the end of each weekly challenge, images will be curated to a Storify and the link will be archived on the Summer Math Photo Challenge website. |
Semaine 9
Relations partie/tout #partietout #mathphoto15 La semaine dernière, nous avons cherché et trouvé des unités. Une douzaine d’oeufs est un tout composé d’unités, tout comme un mur peut être composé de briques. Nous avons aussi trouvé des objets décomposés en parties comme une miche de pain tranchée. Cette semaine, nous explorons la relation entre des parties et un tout. Deborah Ball définit cette relation (particulièrement en lien avec les fractions) en une “divison d’un tout (quantité) en un certain nombre de parties qui peuvent se faire ainsi :
Comment jouer : Prendre une photo. Afficher la photo sur Twitter ou Instagram avec une légende. Utiliser les deux mots-clic : #mathphoto15 et #partietout. Décrire ce que l’on peut voir dans votre photo. Re-tweeter et partager les photos d’autres internautes si vous le voulez. Encourager vos amis à jouer avec vous! Comment apprécier : Visiter le fil Twitter #mathphoto15 en tout temps. Explorer aussi ce fil sur Flickr. À la fin de chaque défi de la semaine, les images seront organisées dans un Storify et le lien sera affiché sur le site DÉFI MATH PHOTO ÉTÉ 2015. |
Semana 9
Relaciones de parte frente al todo #partetodo #mathphoto15 La pasada semana buscamos y encontramos unidades. Doce huevos son una docena que es una unidad compuesta al igual que un muro -que está hecho de ladrillos- También vimos unidades que se podían partir como una hogaza de pan en rebanadas o una loncha de mortadela. Esta semana vamos a trabajar una idea que está relacionada con la del reto anterior y que es la de las relaciones parte/todo. Deborah Ball define esta relación y la vincula con las fracciones como “dividir una unidad dada en un número de partes dado, lo que incluye:
Qué estamos buscando? ¡Mira a tu alrededor! Además de números (fracciones) piensa en números, formas y magnitudes. Las unidades de medida estandar están por todas partes y Segundos/minutos/horas y días céntimos/euros. Milímetros/centímetros/metros, porciones/pizzas y onzas/tabletas de chocolate serán aceptadas. Cómo participar: Haz una foto. Publícala en Twitter o Instagram. Explíca qué ves o dónde la has hecho. Usa los hastags: #mathphoto15 and #partetodo. Retuitea las fotos de los demás que te gusten y anima a tus amigos a participar. Como ver las fotos: Busca el hilo #mathphoto15 en cualquier momento. También puedes ver las fotos que se van subiendo a Flickr. Al final de la semana las mejores imágenes se seleccionarán en un Storify y se archivarán en la web del Desafío Foto-matemático del verano 2015. |
|
|
|
Week 8
Composed & Partitioned Units #units #mathphoto15 [unit noun a single quantity regarded as a whole]
[composed adj. formed by putting together] Composed units begin with a single thing which we assemble with others of these single things to make a larger unit: the assemblage of units becomes a single whole. Here is an example: |
Semaine 8
Unités composées ou fractionnées #unités #mathphoto15 [unité nom] Élément simple, constitutif d’un ensemble homogène]
[composé adj. Constitué de plusieurs éléments.] Un tout commence par une simple unité assemblée à d’autres unités semblables pour former un tout composé. Voici un exemple: |
Semana 8
Compuesto & Particiones de unidades #unidades #mathphoto15 [unidad mat Cantidad que se toma por medida o término de comparación de las demás de su especie]
[compuesto adj. Agregado de varias cosas que componen un todo] Una unidad compuesta empieza como una unidad que puesta con otras iguales a ella acaban dando una unidad superior. Ejemplo: |
|
The original unit is an egg. The composed unit is 12 of these: a dozen eggs.
[partitioned verb divide into parts] The loaf of bread, below, is not a composed unit because we didn’t make the loaf out of slices. Instead, we started with a loaf and cut it into smaller units. That is the process of partitioning. |
L’unité de base est un oeuf. Le tout composé de 12 oeufs c’est une douzaine d’oeufs.
[fractionné verbe séparer en parties] Le pain ci-dessous n’est pas une unité composée de parties car il n’a pas été fait en assemblant des tranches de pain. Nous avons plutôt commencé avec un tout, un pain, et nous l’avons tranché (parties). Ceci s’apparente à un processus de fractionnement. |
La unidad original es el huevo, la unidad compuesta es la docena, 12 huevos “unitarios” componen una docena
[partición que está dividido en partes] La hogaza de pan no es una unidad compuesta porque no hicimos la hogaza de rebanadas, al revés, iniciamos con la hogaza completa y cortamos cada una de las nuevas unidades. Este proceso relata lo que sería una partición. |
|
Also consider a natural unit which refers to a composed unit that has to be the size that it is, like a pair of shoes or a pair of mittens. Conventional unit refers to a unit that we have agreed to, but which doesn’t have to be the size that it is. For example, depending on where in the world you live your eggs could come in cartons of 10, 12, or even 18.
What are we looking for? This week’s theme is a brain teaser! You could start with units of measure in whichever part of the world you live in, but it could be all sorts of other things: you tet to decide how far to stretch it! What makes a whole? What makes “one”? What is made up of parts? If you need some inspiration watch the video at the top of this challenge {embedded video, One is One...or is it?} How to Play: Take a photo. Post to Twitter or Instagram; adding a caption is highly encouraged. Use both hashtags: #mathphoto15 and #units and state what kind of unit you’re seeing, composed or partitioned. Re-tweet and share others’ photos if you like. Encourage your friends to play! How to View: Visit the #mathphoto15 Twitter stream any time. You can also view the stream on Flickr. At the end of each weekly challenge, images will be curated to a Storify and the link will be archived on the Summer Math Photo Challenge website. (Language for this challenge provided by Christopher Danielson who has much more to say on the topic on his blog Overthinking my Teaching. ) |
Nous pourrions aussi considérer des unités usuelles qui feraient référence à des unités composées à cause de leur usage, telles une paire de souliers ou une paire de mitaines. Des unités conventionelles seraient des groupements acceptés selon notre culture ou notre environnement. Par exemple, dans certains pays, les oeufs sont groupés en boîtes de 10, de 12 de 18, de 24,...
Que cherchons nous? Cette semaine, le thème est une énigme. Vous pourriez commencer avec des unités de mesure utilisées dans votre coin de pays mais vous pourriez aussi étendre cette idée beaucoup plus loin! Quel est le tout? Quelle est l’unité? Qu’est-ce qui est composé de parties? Si vous avez besoin d’inspiration, visionnez le clip vidéo au haut de cette page. Comment jouer: Prendre une photo. Afficher la photo sur Twitter ou Instagram avec une légende. Utiliser les deux mots-clic : #mathphoto15 et #unités. Citer si vous voyez des unités, un tout composé ou un tout fractionné. Re-tweeter et partager les photos d’autres internautes si vous le voulez. Encourager vos amis à jouer avec vous! Comment apprécier: Visiter le fil Twitter #mathphoto15 en tout temps. Explorer aussi ce fil sur Flickr. À la fin de chaque défi de la semaine, les images seront organisées dans un Storify et le lien sera affiché sur le site DÉFI MATH PHOTO ÉTÉ 2015. (Les termes utilisés dans ce défi proviennent de Christopher Danielson qui explore ces idées dans son blogue : Overthinking my Teaching.) |
Consideraremos también unidades naturales al referirnos a unidades compuestas que tienen un tamaño definido, como un par de zapatos o una pareja de guantes. Las unidades convencionales son las que vienen de consensos con los que estamos de acuerdo pero podrían tener otro tamaño. Por ejemplo los huevos en función del lugar donde vivas se encuentran en paquetes de 10, de 12, de 18, de 24...
Qué estamos buscando? El tema de esta semana es todo un reto. Puedes comenzar con unidades de medida del lugar donde vivas, pero pueden ser muchas más cosas: tu decides lo lejos que quieres llegar. ¿Qué cosas hacen una unidad? ¿Qué es uno? ¿Qué está compuesto de partes? Si buscas más inspiración te recomendamos ver el vídeo que hay arriba. Cómo participar: Toma una foto. Súbela a Twitter o Instagram; si dices dónde la has tomado es mejor. Usa los hastags #mathphoto15 y #unidades y argumenta qué clase de unidad, composición o partición estás viendo. Retuitea y comparte las fotos de los demás y anima a tus amigos a participar. Cómo ver lo publicado: Visita el HT #mathphoto15 en Twitter. También en el siguiente enlace de Flickr. Al final de cada reto semanal una selección de imágenes se subirán a Storify y archivarán en la web Desafío Foto-matemático verano 2015. (Los términos del reto de esta semana se deben a Christopher Danielson que tiene mucho más que decur sobre el tema en su blog Overthinking my Teaching.) |
Play Symmetry Artist this week over at Math is Fun!
Read a helpful, visual primer of different
kinds of symmetries!
kinds of symmetries!
|
Week 7
Reflections & Rotations #symmetry #mathphoto15 There is no end to examples of symmetries in the designed and natural world. The most familiar are reflections and rotations, but there are also translation and glide symmetries as well. One of the exciting things about symmetry is that it is built on the concepts of equivalence, specifically congruence and isometry: which of the object’s properties have been preserved in the process of transformation? This is a strong connection to #sameness, our #mathphoto15 challenge from the week of June 29.
What are we looking for? Look for examples of reflection and rotation symmetry in your daily life. For example car hubcaps are delightfully rotational and decorative, but might there be reflectional symmetry present as well? Translational symmetry (a basic motif which repeats itself indefinitely forever, usually horizontally or vertically) might be found in fences or decorative borders. These examples may also exhibit other kinds of symmetry as well so look closely! How to Play: Take a photo. Post to Twitter or Instagram; adding a caption is highly encouraged. Use both hashtags: #mathphoto15 and #symmetry. Re-tweet and share others’ photos if you like. Encourage your friends to play! How to View: Visit the #mathphoto15 Twitter stream any time. You can also view the stream on Flickr. At the end of each weekly challenge, images will be curated to a Storify and the link will be archived on the Summer Math Photo Challenge website. |
Semaine 7
Réflexions et Rotations #symétrie #mathphoto15 Il existe une multitude d’exemples de symétrie dans le monde construit et le monde naturel. Les plus courantes sont les réflexions et les rotations, mais il existe aussi des exemples avec des translations et des glissements. L’idée de la symétrie est liée aux concepts d’équivalence, en particulier la congruence et l’isométrie. Quelles propriétés de la figure sont conservées lorqu’elle subit de telles transformations? Il y a un lien avec notre thème de #similitude, notre défi #mathphoto15 de la semaine du 29 juin.
Que cherchons nous? Cherchez des exemples de réflexions et de symétrie dans votre quotidien. Par exemple, les enjoliveurs de roues sont décoratifs et subissent des rotations. Toutefois, pouvez-vous aussi y trouver une symétrie axiale? Une symétrie orthogonale ou un motif qui subit plusieurs translations peut être trouvée dans des clôtures ou des bordures décoratives. Vos exemples peuvent aussi démontrer différents types de symétrie alors soyez aux aguets! Comment jouer: Prendre une photo. Afficher la photo sur Twitter ou Instagram. Utiliser les deux mots-clic : #mathphoto15 et #symétrie. Re-tweeter et partager les photos d’autres internautes si vous le voulez. Encourager vos amis à jouer avec vous! Comment apprécier: Visiter le fil Twitter #mathphoto15 en tout temps. Explorer aussi ce fil sur Flickr. À la fin de chaque défi de la semaine, les images seront organisées dans un Storify et le lien sera affiché sur le site DÉFI MATH PHOTO ÉTÉ 2015. |
Semana 7
Reflexiones y rotaciones #simetria #mathphoto15 Existe una multitud de ejemplos de simetrías en el mundo construido y en el mundo natural. Las más corrientes son las reflexiones y las rotaciones, pero también existen traslaciones y simetrías con deslizamiento. Una de las cosas más sorprendentes sobre la simetría es que se define a partir de conceptos de equivalencia, específicamente congruencia e isometría: ¿qué propiedades del objeto se deben preservar en el proceso de transformación? Esta es una conexión importante a #similitud, nuestro desafío #mathphoto15 de la semana del 29 de junio.
Qué estamos buscando? Busca ejemplos de simetrías de reflexión o rotación en tu vida diaria. Por ejemplo, los tapacubos de los coches son deliciosamente rotacionales y decorativos, pero ¿tienen un eje de simetría también? La simetría de traslación (un motivo básico que se repite indefinidamente, normalmente en horizontal o en vertical) se suele encontrar en las verjas o en las cenefas decorativas. Estos ejemplos también pueden tener otros tipos de simetría, así que ¡observa atentamente! Cómo participar: Toma una foto, compártela en Twitter o Instagram, si es posible con una descripción. Utiliza los hashtags: #mathphoto15 y #simetría. Retuitea y comparte las fotos de los demás si te gustan. ¡Anima a tus amigos a participar! Cómo visualizar: Visita #mathphoto15 en Twitter en cualquier momento. También puedes ver todas las aportaciones en Flickr. Al final de cada desafío semanal, las imágenes serán seleccionadas en un Storify y el enlace se archivará en la web del Desafío Foto-matemático verano 2015. |
|
Week 6
Shape & Number #numbershape #mathphoto15 Shapes are all around us. Geometric shapes may have two dimensions: length and width. They may have more.They might be the familiar simple shapes of the maths lesson, or the more organic hard-to-define ones we see in the street or park.
Throughout history, geometry and number have been inextricably linked. Think of the word figure. What does it mean? Someone’s shape? A written number? Or “figuring out”? The Greeks, starting, legend has it, with Pythagoras, explored numbers figurately, learning about their character through their disposition in space. Whereas in the present day we tend to think of square number as a number multiplied by itself, for the Greeks a square number could be serried rows of pebbles in the shape of a square (the word “calculation” comes from the word for a pebble, khalix). The development of algebra in medieval Baghdad and beyond could be seen as a departure from the geometrical. But the two were never far apart. And Descartes in the 17th century made a new bond, representing algebraic expressions on the coordinate plane that is named for him. Equations became shapes; shapes became equations. What are we looking for? Mathematicians have continued to find surprising links between geometry and number. What links can you see between the two? What shapes can you spot that are created by the arrangement of a number of objects? How many parts do you see in a shape you notice? What other numerical features might it have? Explore the intersection of number and shape generously and serendipitously. And don’t forget the hashtags: #mathphoto15 and #numbershape How to Play: Take a photo. Post to Twitter or Instagram. Use both hashtags: #mathphoto15 and #numbershape. Re-tweet and share others’ photos if you like. Encourage your friends to play! How to View: Visit the #mathphoto15 Twitter stream any time. You can also view the stream on Flickr. At the end of each weekly challenge, images will be curated to a Storify and the link will be archived on the Summer Math Photo Challenge website. |
Semaine 6
Formes et nombres #nombreforme #mathphoto15 Les formes sont partout autour de nous. Les figures géométriques peuvent avoir deux dimensions: longueur et largeur. Elles peuvent en avoir davantage. Elles peuvent être les figures courantes de nos leçons de mathématiques ou les figures plus organiques plus difficiles à définir que l’on voit dans la rue ou au parc.
À travers l’histoire, les nombres et la géométrie ont été emmêlés. Les Grecs tels Pythagore, selon la légende, auraient exploré les nombres en lien avec leur disposition dans l’espace. Alors qu’on pense souvent à un nombre carré comme un nombre multiplié par lui-même, pour les Grecs, ce nombre était une organisation de rangées de cailloux en forme de carré. (Le mot calcul est dérivé du mot latin “calculus” qui signifie “petit caillou”) Le développement de l’algèbre pourrait être vu comme un éloignement de la géométrie, mais les deux domaines ne sont jamais bien loin l’un de l’autre. Descartes, au 17e siècle, représente des expressions algébriques le plan qui porte son nom. Les équations deviennent alors des formes et les formes, des équations. Que cherchons nous? Les mathématiciens ont observé des liens étonnants entre la géométrie et les nombres au fil du temps. Quels liens voyez-vous entre les deux? Quelles formes pouvez-vous dénicher qui sont créées par l’arrangement d’un certain nombre d’objets? Combien de parties voyez-vous dans les formes que vous remarquez? Quelles autres particularités numériques ont-elles? Explorez les liens entre les nombres et les formes sans limites. N’oubliez pas les mots-clic #mathphoto15 et #nombreforme Comment jouer: Prendre une photo. Afficher la photo sur Twitter ou Instagram. Utiliser les deux mots-clic : #mathphoto15 et #nombreforme. Re-tweeter et partager les photos d’autres internautes si vous le voulez. Encourager vos amis à jouer avec vous! Comment apprécier: Visiter le fil Twitter #mathphoto15 en tout temps. Explorer aussi ce fil sur Flickr. À la fin de chaque défi de la semaine, les images seront organisées dans un Storify et le lien sera affiché sur le site DÉFI MATH PHOTO ÉTÉ 2015. |
Semana 6
Forma y número #formanumero #mathphoto15 Las formas nos rodean. Las formas geométricas pueden tener dos dimensiones (ancho y alto) pero también pueden tener más. Pueden ser las muy familiares figuras simples de clase de matemáticas o las formas orgánicas mucho más difíciles de definir que podemos ver por la calle o en la naturaleza.
A lo largo de la Historia la geometría y los números han estado vinculados. Los antiguos griegos no podían separar los números de la representación organizada de estos. Por eso hablaban de números cuadrados, rectangulares, triangulares... Hoy tendemos a pensar que un número es un cuadrado si hay otro número que multiplicado por si mismo da el primero pero ellos llamaban "cuadrado" al número que representado por piedrecitas -los calculus romanos- admitía una configuración con forma de cuadrado. El desarrollo del álgebra en la Persia medieval partió también de lo geométrico y discurrió en paralelo al desarrollo de la geometría, en el siglo XVII Descartes las unió para siempre situando las expresiones algebraicas en el plano coordenado (que por algo se llama cartesiano). A partir de Descartes, las ecuaciones se representarán como formas, las formas se corresponderán con ecuaciones. Qué estamos buscando? Los matemáticos seguimos encontrando relaciones sorprendentes entre geometría y números ¿cuáles encuentras tu?¿Qué formas encuentras que se puedan crear organizando objetos?¿Cuántas partes puedes ver en una forma?¿Qué otras características numéricas tiene? Te invitamos a explorar la intersección entre número y forma con curiosidad y generosidad, y no olvides los hashtags: #mathphoto15 y #formanumero. Retuitea y comparte las fotos de los demás, si quieres. ¡Anima a tus amigos a participar! ¿Cómo participar? Haz una foto. Compártela en Twitter o Instagram. Utiliza ambos hashtags: #mathphoto15 y #formanumero. Retuitea y comparte las fotos de los demás, si quieres. ¡Anima a tus amigos a participar! Cómo ver: Visita #mathphoto15 en Twitter en cualquier momento. También puedes ver todas las aportaciones en Flickr. Al final de cada desafío semanal, las imágenes serán seleccionadas en un Storify y el enlace se archivará en la web del Desafío Foto-matemático verano 2015. |
|
Week 5
Equivalence (Congruent, similar & equal) #sameness #mathphoto15 Equivalence is an overarching idea that includes equality (numerical sameness), similarity, and congruence (geometric sameness). In all three there is at least one thing or idea in common with another thing/idea. For example, cats and dogs are not the same...or are they? Both cats and dogs are similar because they both have two ears, tails, four legs, they’re both mammals, etc. Noticing sameness, similarity or even its opposite, outright difference between things is what this week’s challenge is all about.
What are we looking for? You can approach this week’s challenge in so many ways. A great starting point is finding examples of what #sameness isn’t. Why not begin by looking for logical opposites (short/tall, big/little, hot/cold)? Once you’ve got the hang of that start looking for what those opposites have in common. How to Play: Take a photo. Post to Twitter or Instagram. Use both hashtags: #mathphoto15 and #sameness. Tell us what kind of sameness you see! Re-tweet and share others’ photos if you like. Encourage your friends to play! How to View: Visit the #mathphoto15 Twitter stream any time. You can also view the stream on Flickr. At the end of each weekly challenge, images will be curated to a Storify and the link will be archived on the Summer Math Photo Challenge website. |
Semaine 5
Équivalence (Congruent, semblable,égalité) #similitude L’équivalence est une grande idée qui inclut l’égalité, une affirmation que deux expressions mathématiques représentent la même quantité (numérique ou algébrique), la congruence (une équivalence géométrique) et ainsi que des notions de similitude. Dans ces trois concepts, il y a au moins une idée ou un élément qui est équivalent à une autre idée ou élément. Par exemple, les chiens et les chats ne sont pas pareils … ou le sont-ils? Les deux sont des mammifères qui ont chacun, deux oreilles, une queue, quatre pattes etc. Remarquer ce qui est équivalent, semblable ou même l’opposé est l’objectif du défi de cette semaine.
Que cherchons nous? Il y a différentes façons d’aborder le défi. Considérez chercher des exemples où des objets n’ont aucune #similitude. Pourquoi ne pas chercher des opposées (court/long, gros/mince, chaud/froid)? Par la suite, mettez vous à analyser ce que ces choses ont en commun. Comment jouer: Prendre une photo. Afficher la photo sur Twitter ou Instagram. Utiliser les deux mots-clic : #mathphoto15 et #similitude. Re-tweeter et partager les photos d’autres internautes si vous le voulez. Encourager vos amis à jouer avec vous! Comment apprécier : Visiter le fil Twitter #mathphoto15 en tout temps. Explorer aussi ce fil sur Flickr. À la fin de chaque défi de la semaine, les images seront organisées dans un Storify et le lien sera affiché sur le site DÉFI MATH PHOTO ÉTÉ 2015. |
Semana 5
Equivalencia (Congruente, similar e igual) #similitud La equivalencia es una idea general que incluye la igualdad (similitud numérica), similaridad, y congruencia (similitud geométrica). En las tres al menos hay una idea en común con otra idea. Por ejemplo, perros y gatos no son iguales… ¿o sí? Ambos son similares porque tienen cuatro patas, dos orejas, cola, son mamíferos, etc. Darse cuenta de la igualdad, la similaridad o incluso lo que es opuesto, recalcando las diferencias entre cosas es de lo que va el desafío de esta semana.
¿Qué estamos buscando? Las propuestas de esta semana pueden ser desde muchos puntos de vista. Un buen inicio es buscar ejemplos de lo que no es la #similitud. ¿Por qué no empezar buscando opuestos lógicos (alto/bajo, pequeño/grande, frío/caliente)? Una vez que tengas esto claro, luego podrás buscar qué es lo que tienen estos opuestos en común. ¿Cómo participar? Haz una foto. Compártela en Twitter o Instagram. Utiliza ambos hashtags: #mathphoto15 y #similitud. ¡Dinos qué tipo de similitud ves! Retuitea y comparte las fotos de los demás, si quieres. ¡Anima a tus amigos a participar! Cómo ver: Visita #mathphoto15 en Twitter en cualquier momento. También puedes ver todas las aportaciones en Flickr. Al final de cada desafío semanal, las imágenes serán seleccionadas en un Storify y el enlace se archivará en la web del Desafío Foto-matemático verano 2015. |
|
Week 4
Three #three #mathphoto15 This week’s challenge is “three”. How many different instances of three can you find?
How to Play: Take a photo. Post to Twitter or Instagram. Use the hashtags: #mathphoto15 and #three. Re-tweet and share others’ photos if you like. Encourage your friends to play! How to View: Visit the #mathphoto15 Twitter stream any time. You can also view the stream on Flickr. At the end of each weekly challenge, images will be curated to a Storify and the link will be archived on the Summer Math Photo Challenge website. |
Semaine 4
Trois #trois #mathphoto15 Le défi cette semaine est “trois”. Combien de différentes exemples de trois pouvez-vous trouver?
Comment jouer: Prendre une photo. Afficher la photo sur Twitter ou Instagram. Utiliser les deux mots-clic : #mathphoto15 et #trois. Re-tweeter et partager les photos d’autres internautes si vous le voulez. Encourager vos amis à jouer avec vous! Comment apprécier: Visiter le fil Twitter #mathphoto15 en tout temps. Explorer aussi ce fil sur Flickr. À la fin de chaque défi de la semaine, les images seront organisées dans un Storify et le lien sera affiché sur le site DÉFI MATH PHOTO ÉTÉ 2015. |
Semana 4
Tres #tres #mathphoto15 El desafío de esta semana es “tres”. ¿Cuantos treses diferentes puedes encontrar?
Cómo participar: Haz una foto. Compártela en Twitter o Instagram. Utiliza los hashtags: #mathphoto15 y #tres. Retuitea y comparte las fotos de los demás si quieres. ¡Anima a tus amigos a participar! Cómo ver: Visita #mathphoto15 en Twitter en cualquier momento. También puedes ver todas las aportaciones en Flickr. Al final de cada desafío semanal, las imágenes serán seleccionadas en un Storify y el enlace se archivará en la web del Desafío Foto-matemático verano 2015. |
|
|
|
Week 3
Tesselations #tiles #mathphoto15 A tessellation is created when a shape is repeated over and over again covering a plane without any gaps or overlaps. People have been making tessellations long for a long time. Five millenia ago, the Sumerians were creating repeating patterns with tiles. Perhaps the most beautiful examples of tessellation are more recent, including the complex tilings developed in the Muslim world. The 14th-century tiling patterns at the Alhambra Palace in Granada in Spain for instance are a wonder of tessellation.
In 1891, Yevgraf Fyodorov proved that every periodic tiling of the plane features one of seventeen different “wallpaper groups”. These patterns are to be found everywhere - on pottery or paving, in brickwork and, of course, wallpaper. What are we looking for? Can you spot a pattern of repeating shapes that cover a plane without gaps or overlaps? There are also frieze patterns which are 2D patterns that only repeat in one direction. And what about three dimensional tessellations--solid shapes that completely fill a 3D space without gaps or overlaps? What can you find? Snap it up! Don’t forget to use the hashtags #mathphoto15 and #tiles. How to Play: Take a photo. Post to Twitter or Instagram. Use both hashtags: #mathphoto15 and #tiles. Re-tweet and share others’ photos if you like. Encourage your friends to play! How to View: Visit the #mathphoto15 Twitter stream any time. You can also view the stream on Flickr. At the end of each weekly challenge, images will be curated to a Storify and the link will be archived on the Summer Math Photo Challenge website. |
Semaine 3
Tesselations #dallages #mathphoto15 Un dallage (ou pavage) est créé lorsque des figures recouvrent un plan sans espaces libres ni superpositions des figures. Depuis très longtemps, les gens ont réalisé des dallages. Il y a cinq mille ans, les Sumériens produisaient des motifs répétés avec des tuiles. Parmi les plus beaux exemples récents, on retrouve les dallages complexes de la civilisation islamique. Les mosaïques du palais Alhambra à Grenade en Espagne, produites au XIVe siècle, contiennent presque tous les types de pavages.
En 1891, Yevgraf Fyodorov a démontré qu’il existe 17 types de pavage du plan. Ces motifs se retrouvent partout : sur la poterie ou les pavages, dans la maçonnerie et le papier peint. Ce que l’on cherche? Pouvez-vous dénicher des dallages composés de figures recouvrant un plan sans espace libre ni superposition? Nous cherchons aussi des frises qui sont des bandes continues et ordonnées sur lesquelles un motif se répète de façon régulière. Et pourquoi pas des compositions en trois dimensions sans espaces ni superpositions? Que pouvez-vous trouver? Captez ces images! Pensez à utiliser les mots clic #mathphoto15 et #dallages Comment jouer: Prendre une photo. Afficher la photo sur Twitter ou Instagram. Utiliser les deux mots-clic : #mathphoto15 et #dallage. Re-tweeter et partager les photos d’autres internautes si vous le voulez. Encourager vos amis à jouer avec vous! Comment apprécier: Visiter le fil Twitter #mathphoto15 en tout temps. Explorer aussi ce fil sur Flickr. À la fin de chaque défi de la semaine, les images seront organisées dans un Storify et le lien sera affiché sur le site DÉFI MATH PHOTO ÉTÉ 2015. |
Semana 3
Tesselations #teselaciones #mathphoto15 Una teselación se crea cuando una forma se repite una y otra vez cubriendo el plano sin espacios vacíos ni superposiciones. La humanidad ha estado creando teselaciones desde hace mucho tiempo. Hace cinco milenios los sumerios crearon mosaicos con baldosas. Quizás los ejemplos más bonitos de teselaciones son más recientes, incluyendo las baldosas complejas desarrolladas en el mundo musulmán. Los mosaicos del siglo XIV del Palacio de la Alhambra en España son un ejemplo maravilloso de teselación.
En 1891 Yevgraf Fyodorov demostró que cada teselación del plano coincide con uno de los 17 diferentes “grupos cristalográficos”. Estos mosaicos se pueden encontrar en cualquier sitio: en la cerámica o pavimentación, en ladrillo y, por supuesto, en papel de pared. ¿Qué estamos buscando? ¿Puedes encontrar un mosaico de figuras repetidas que cubra el plano sin espacios o superposiciones? Busca también frisos, que son patrones en 2D que se repiten en una dirección. ¿Y por qué no teselaciones en tres dimensiones - cuerpos sólidos que rellenan completamente un espacio 3D sin agujeros ni superposiciones? ¿Qué puedes encontrar? ¡Vamos! No olvides usar los hashtags #mathphoto15 y #teselaciones. Cómo participar: Haz una foto. Compártela en Twitter o Instagram. Utiliza ambos hashtags: #mathphoto15 y #teselaciones. Retuieta y comparte las fotos de los demás si te gustan. ¡Anima a tus amigos a participar! Cómo ver: Visita #mathphoto15 en Twitter en cualquier momento. También puedes ver todas las aportaciones en Flickr. Al final de cada desafío semanal, las imágenes serán seleccionadas en un Storify y el enlace se archivará en la web del Desafío Foto-matemático verano 2015. |
|
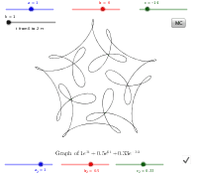
Play around with this fun curve!
Jouez avec cette courbe de plaisir! ¡Juega un poco con esta curva divertida! |
|
Week 2
Lines and Curves #lines #mathphoto15 Lines and curves are the building blocks of visual representations in mathematics. A number line is a simple line that can help us understand the relationships between numbers. Lines are also useful for constructing and deconstructing geometric shapes. On a coordinate plane graphed lines and curves help us visualize and describe relationships between two quantities; these visualizations are sometimes elegant and worth appreciating in and of themselves.
What are we looking for? This week, we are looking for examples of, and interesting juxtapositions between lines and curves in our everyday life. Look for spirals, curves, and lines in relationship to one another (perpendicular, parallel, tangent, etc.) Keep your eye out for non-examples. What do you see that is not a line or a curve? Ask your kids (or yourself!) how they know it is or isn’t a line. You might just spark some fun conversations! How to Play: Take a photo. Post to Twitter or Instagram. Use both hashtags: #mathphoto15 and #lines. Re-tweet and share others’ photos if you like. Encourage your friends to play! How to View: Visit the #mathphoto15 Twitter stream any time. You can also view the stream on Flickr. At the end of each weekly challenge, images will be curated to a Storify and the link will be archived on the Summer Math Photo Challenge website. Week 1
Arrays & Grids #array #mathphoto15 Spatial concepts underlie much of mathematics and, by extension, mathematical reasoning. An array is a spatial construct that can help us illustrate and make sense of quantity, multiplication, division, and area. Grids are a useful visual/spatial tool for analyzing change and relationships. Both arrays and grids help learners develop understanding of number, operations and their properties.
What are we looking for? This week, look for examples of arrays and grids in your everyday life and travels. Keep your eye out for non-examples. Ask your kids (or yourself!) how they know it’s an array. You might just spark some fun math-y conversations. How to Play: Take a photo. Post to Twitter or Instagram. Use both hashtags: #mathphoto15 and #array. Re-tweet and share others’ photos if you like. Encourage your friends to play too! How to View: Visit the #mathphoto15 Twitter stream any time. You can also view the stream on Flickr. At the end of each weekly challenge, images will be curated to a Storify and the link will be archived on the Summer Math Photo Challenge website. |
Semaine 2
Droites et courbes #lignes #mathphoto15 Les droites et les courbes sont des éléments de base des représentations visuelles en mathématiques. Une droite numérique est une ligne simple qui nous aide à comprendre les relations entre les nombres. Les lignes sont aussi utiles pour construire et décomposer des formes géométriques. Sur un plan cartésien, des droites et des courbes nous permettent de visualiser et de décrire la relation entre deux entités; ces représentations visuelles sont parfois élégantes et dignes d’admiration en soi.
Ce que l’on cherche? Cette semaine, ce sont des exemples de juxtapositions intéressantes de lignes et de courbes dans votre environnement. Chercher des spirales, des lignes courbes et des lignes en relation avec d’autres lignes (perpendiculaires, parallèles, tangentes). Garder l’oeil ouvert pour des contre-exemples. Poser les questions : “Que voit-on qui n’est pas une ligne ou une courbe? ” et “Comment le sais-tu? ”. Susciter des jasettes mathématiques dans votre entourage. Comment jouer: Prendre une photo. Afficher la photo sur Twitter ou Instagram. Utiliser les deux mots-clic : #mathphoto15 et #lignes. Re-tweeter et partager les photos d’autres internautes si vous le voulez. Encourager vos amis à jouer avec vous! Comment apprécier: Visiter le fil Twitter #mathphoto15 en tout temps. Explorer aussi ce fil sur Flickr. À la fin de chaque défi de la semaine, les images seront organisées dans un Storify et le lien sera affiché sur le site DÉFI MATH PHOTO ÉTÉ 2015. Semaine 1
Dispositions organisées #disposition #mathphoto15 Les concepts liés au raisonnement spatial font partie intrinsèque de l’apprentissage mathématique.
Une disposition organisée nous aide à discerner aisément des quantités, à déterminer des aires et à représenter des situations de multiplication et de division. Des représentations visuelles bien structurées (réseaux, grilles, matrices, étalages...) facilitent l’analyse des relations, des régularités et des changements. Ce que l’on cherche? Cette semaine, chercher des exemples de dispositions rectangulaires ou circulaires dans votre environnement. Garder l’oeil ouvert pour des contre-exemples. Poser la question : “Est-ce une disposition organisée?”. Susciter des jasettes mathématiques dans votre entourage. Comment jouer: Prendre une photo. Afficher la photo sur Twitter ou Instagram. Utiliser les deux mots-clic : #mathphoto15 et #dispositions. Re-tweeter et partager les photos d’autres internautes si vous le voulez. Encourager vos amis à jouer avec vous! Comment apprécier: Visiter le fil Twitter #mathphoto15 en tout temps. Explorer aussi ce fil sur Flickr. À la fin de chaque défi de la semaine, les images seront organisées dans un Storify et le lien sera affiché sur le site Site DÉFI MATH PHOTO ÉTÉ 2015 . |
Semana 2
Líneas rectas y curvas #lineas # mathphoto15 Las líneas rectas y curvas son elementos básicos de las representaciones visuales en matemáticas. Una línea numérica es una línea simple que nos puede ayudar a entender las relaciones entre números. Las líneas son también útiles para construir y descomponer formas geométricas. Sobre el plano cartesiano, las líneas nos ayudan a describir relaciones entre dos cantidades; estas visualizaciones son en ocasiones elegantes y vale la pena estudiarlas por si mismas.
¿Qué estamos buscando? Esta semana, buscamos ejemplos de líneas rectas y curvas en nuestra vida cotidiana. Busca espirales, curvas y líneas relacionadas con otras (perpendiculares, paralelas, tangentes, etc.) Mantén tus ojos abiertos para contraejemplos. Pregunta a tus hijos (¡o a ti mismo!) ¿Cómo sabéis que es una línea? Se pueden provocar algunas conversaciones muy divertidas. Cómo participar: Haz una foto. Publícala en Twitter o Instagram. Usa los dos hashtags: #mathphoto15 y #lineas. Retuitea y comparte fotos de los demás, si quieres. ¡Anima a tus amigos a participar! Cómo ver: Visita el hashtag #mathphoto15 en cualquier momento. También puedes ver los aportes de los demás en Flickr. Al final de cada desafío semanal, las imágenes se añadirán a un Storify y el vínculo se archivará en el sitio web del Desafío foto-matemático verano 2015. Semana 1
Matrices y cuadrículas #matrices # mathphoto15 Conceptos espaciales subyacen bajo gran parte de las matemáticas y, por extensión, al razonamiento matemático. Una matriz es una construcción espacial que puede ayudar a ilustrar y dar sentido a la cantidad, la multiplicación, la división y el área. La disposición en cuadrícula es una herramienta visual y espacial muy útil para analizar el cambio y las relaciones. Las matrices y la disposición en red ayudan a los estudiantes a desarrollar la comprensión del número, las operaciones y sus propiedades.
¿Qué estamos buscando? Esta semana, busca ejemplos de matrices y disposición en red en tu vida. Mantén tus ojos abiertos para contraejemplos. Pregunta a tus hijos (¡o a ti mismo!) ¿Cómo sabéis que es una matriz? Se pueden provocar algunas conversaciones matemáticas muy divertidas. Cómo participar: Toma una foto. Publícala en Twitter o Instagram. Usa los dos hashtags: #mathphoto15 y #matrices. Retuitea y comparte fotos de los demás, si quieres. ¡Anima a tus amigos a jugar también! Cómo ver: Visita el hashtag #mathphoto15 en cualquier momento. También puedes ver los aportes de los demás en Flickr. Al final de cada desafío semanal, las imágenes se añadirán a un Storify y el vínculo se archivará en el sitio web del Desafío foto-matemático verano 2015. |